• $N$ corrupted observations $S=\{{\mathbf{N}}_i|i\in [1,N]\}$ of an uncorrupted 3D shape or scene $\mathbf{S}$
• Learn SDF $f$ of $\mathbf{S}$ from $S$ without ground truth signed distances, point normals, or clean point clouds
  • For a query location $\mathbf{q}\in {\mathbb{R}}^3$ around $\mathbf{S}$, train a neural network parameterized by $\theta$ to learn $f$

Find the uncorrupted point cloud ${\mathit{N}}^{\prime }$ from its corrupted observations $\mathit{N}\in \mathit{S}$ below,

$$\underset{F}{\mathrm{argmin}}\sum _{{\mathit{N}}_i\in S}\sum _{{\mathit{N}}_j\in S}L(F\left({\mathit{N}}_i\right),{\mathit{N}}_j).$$

1. For 2D images, multiple corrupted observations have the pixel correspondence. This results in an assumption that all noisy observations at the same pixel location are ran- dom realizations of a distribution around a clean pixel value. However, this assumption is invalid for point clouds.
2. How to learn SDF $f$ via point cloud denoising

There are many potential paths to achieve this, but only one path is the shortest to the surface. Then involving with SDF, make the denosing function find the shortest path
For an arbitrary point $n$ on the noisy point cloud $\mathbf{N}$, define the denosing funtion below,

where $d=f_{\mathit{\theta }}(\mathit{n},\mathit{c})$

Conclusion : EMD is the better distance metric for comparing nosiy point cloud $\mathbf{N}$ and the underlying clean point cloud ${\mathbf{N}}^{\prime }$

• (a) Nosiy Point Cloud
• (b) Denosing Point Cloud by CD
• (c) Denosing Point Cloud by EMD
• (d) Reconstructed Mesh by MatchingCubes algorithm according the learned SDF (CD) without Geometric Consistency
• (e) Reconstructed Mesh by MatchingCubes algorithm according the learned SDF (EMD) without Geometric Consistency
• (f) Denosing Point Cloud by EMD with Geometric Consistency
• (g) Reconstructed Mesh by MatchingCubes algorithm according the learned SDF (EMD) with Geometric Consistency
• (h) Ground truth

Refer (b) and (c), $\underset{\theta }{min}\sum _{{\mathit{N}}_i\in S}\sum _{{\mathit{N}}_j\in S}L(F({\mathit{N}}_i,f_{\mathit{\theta }}),{\mathit{N}}_j)$ constrains that points on the noisy point cloud should arrive onto the surface but there are no constraints on the paths to be the shortest. one situation that may happen is shown in (b), With the wrong signed distances $f(\theta )$ and gradient $\mathrm{\nabla }{f}_{\mathit{\theta }}$, noises can also get pulled onto the surface, which results in a denoised point cloud with zero EMD distance to the clean point clouds. This is much different from the correct signed distance field that we expected in (c)

for an arbitrary query $\mathbf{n}$ around a noisy point cloud ${\mathbf{N}}_i$, the shortest distance between $\mathbf{n}$ and the surface can be either predicted by the SDF $f_{\theta }$ or calculated based on the denosied point cloud ${\mathit{N}}_i^{\prime }=F({\mathit{N}}_i,f_{\theta })$, both of which should be consistent to each other.

• Therefore,the absolute value $|f_{\theta }(\mathit{n},\mathit{c})|$ of the signed distance predicted at $\mathbf{n}$ should equal to the minimum distance between $\mathbf{n}$ and the denosied point cloud ${\mathbf{N}}^{\prime }=F({\mathbf{N}}_i,f_{\theta })$, Since the point density of ${\mathit{N}}_i^{\prime }$ may slightly affect the consistency, we leverage an inequality to describe the geometric consistency,
• $$|f_{\theta }(\mathit{n},\mathit{c})|\le \underset{{\mathit{n}}^{\prime }\in F({\mathit{N}}_i,f_{\theta })}{min}{\Vert \mathit{n}-{\mathit{n}}^{\prime }\Vert }_2$$

$$\underset{\theta }{min}\sum _{{\mathit{N}}_i\in S}(\sum _{{\mathit{N}}_j\in S}L(F({\mathit{N}}_i,f_{\theta }),{\mathit{N}}_j)+\frac{\lambda }{\left|{\mathit{N}}_i\right|}\sum _{\mathit{n}\in {\mathit{N}}_i}R(E)),$$

where

• $E=(|f_{\theta }(\mathit{n},\mathit{c})|-\underset{{\mathit{n}}^{\prime }\in F({\mathit{N}}_i,f_{\theta })}{min}{\Vert \mathit{n}-{\mathit{n}}^{\prime }\Vert }_2)$
• $R(E)=max(0,E)$
• Comparing (c) and (f), with Geometric Consistency, the denoising Point Cloud are more uniformly distributed.
• Comparing (e) and (g), learn a correct SDF to reconstruct plausible surface.

3 queries (black cubes) sampled from one noisy point cloud get pulled onto the surface

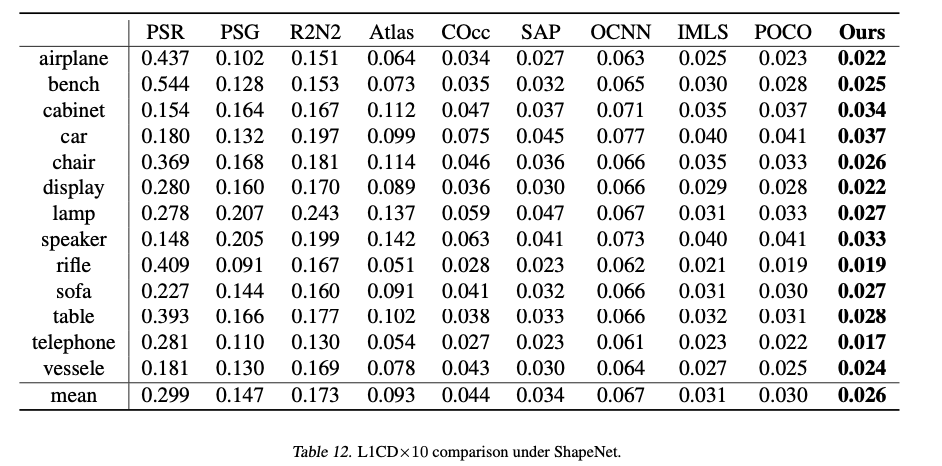
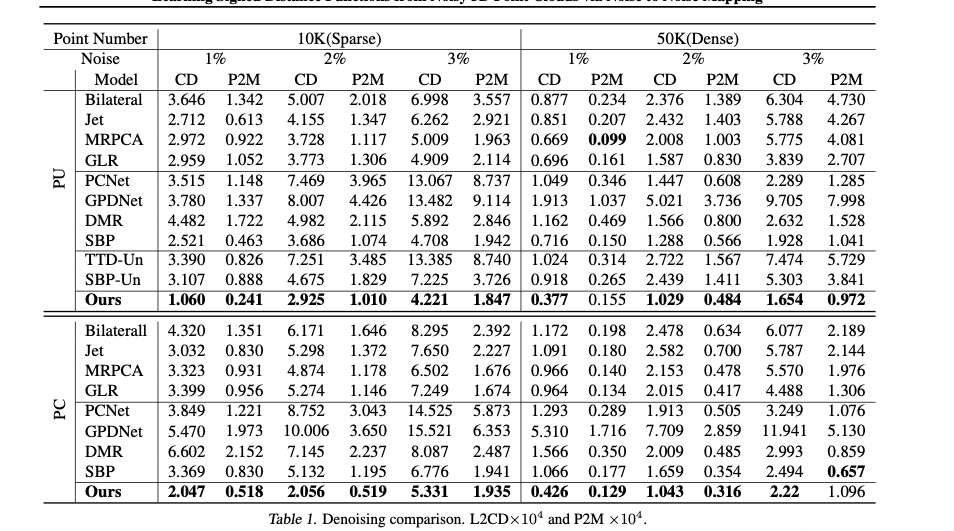
• Datasets: PU(PUNet) and PC(PointCleanNet)
  

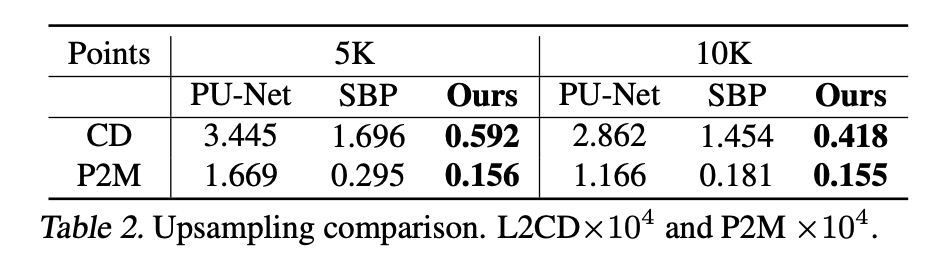
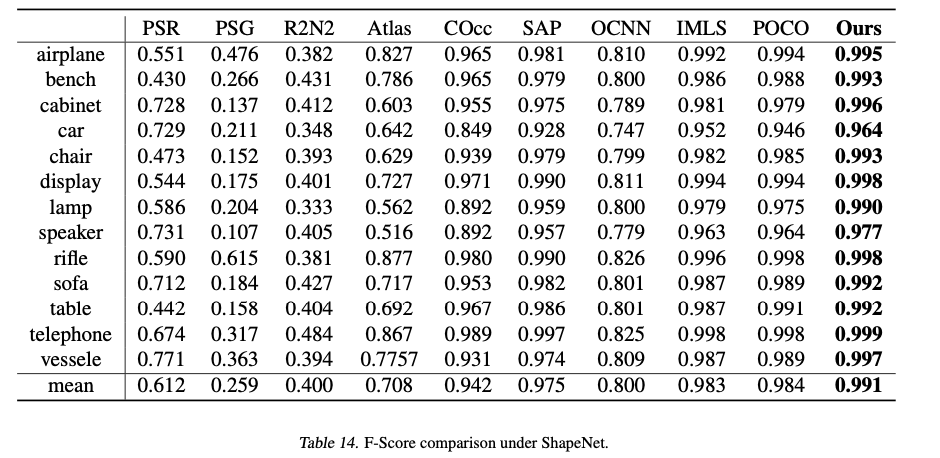
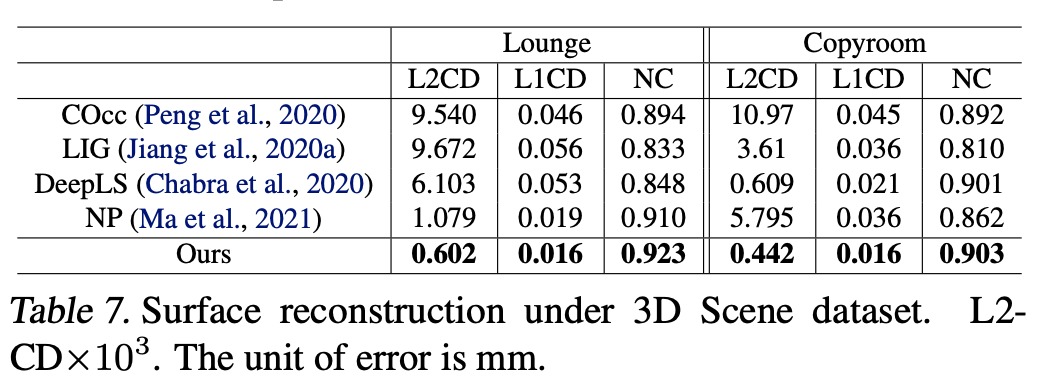
Datasets: ShapeNet

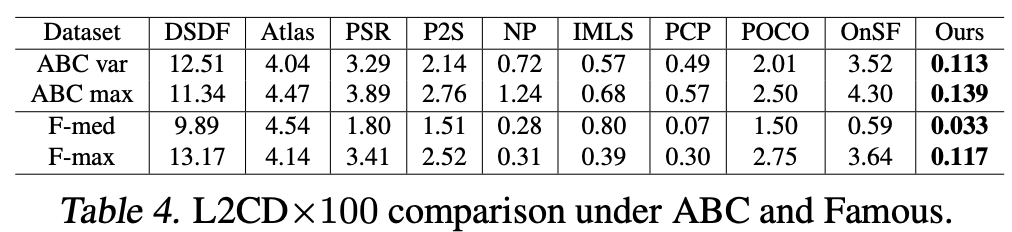
• Dataset: FAMOUS and ABC.
  
  

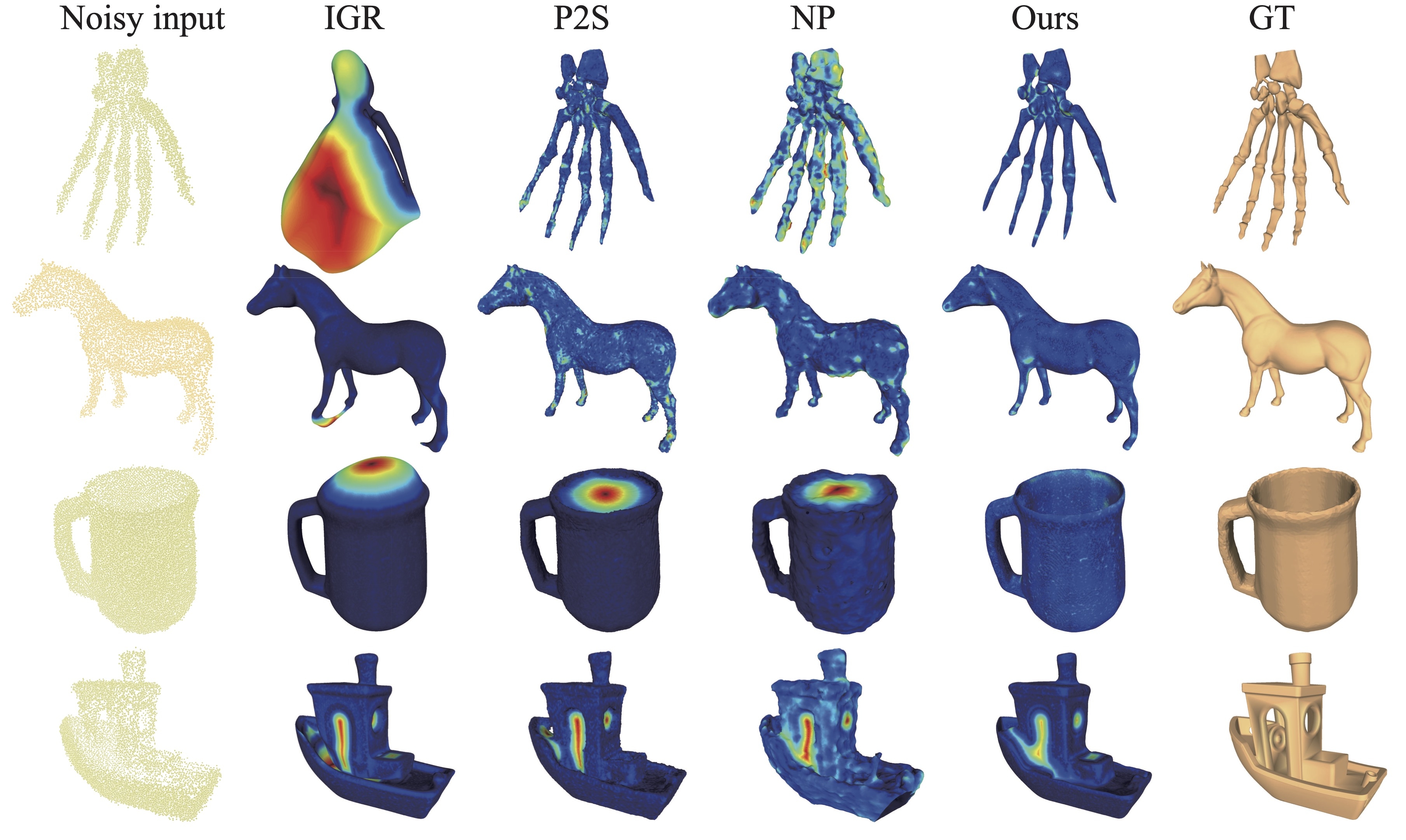
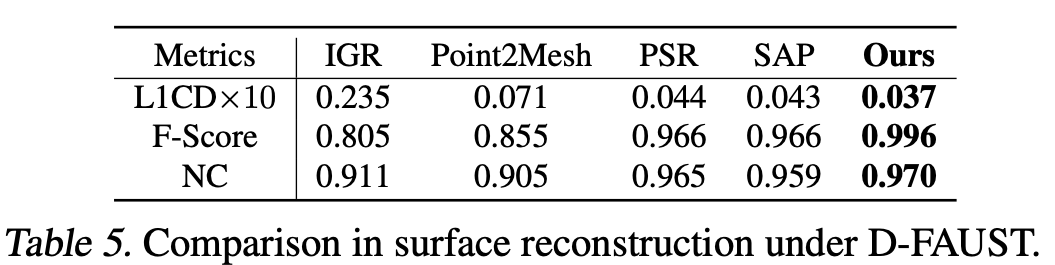
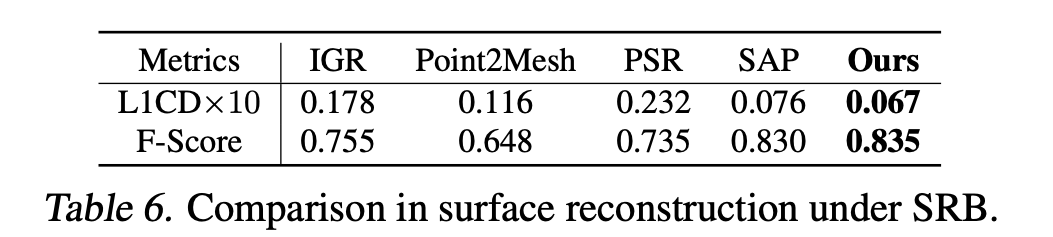
• Dataset: D-FAUST and SRB
  
  
  

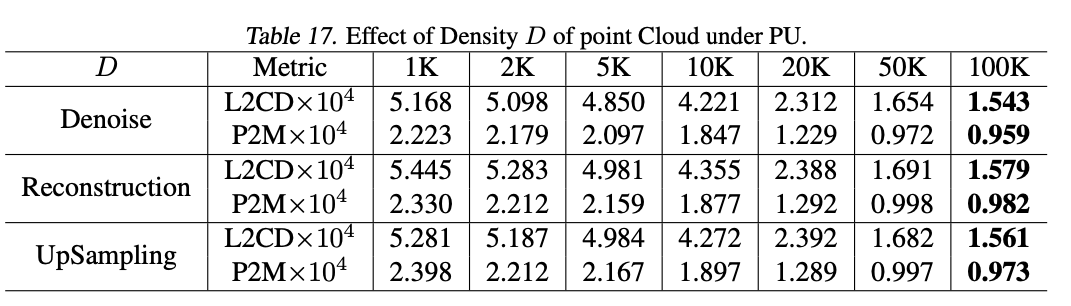
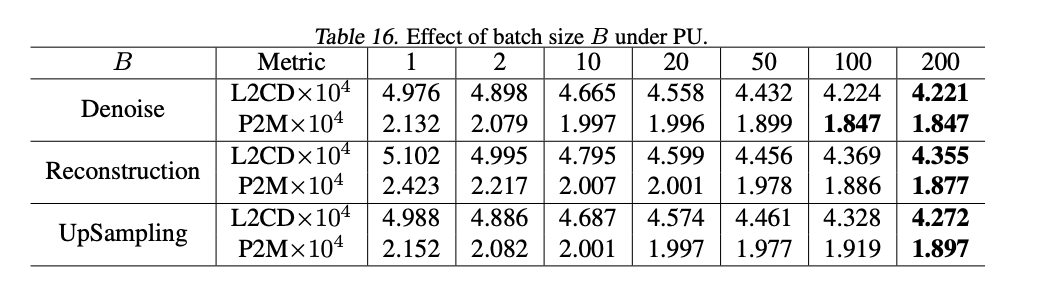
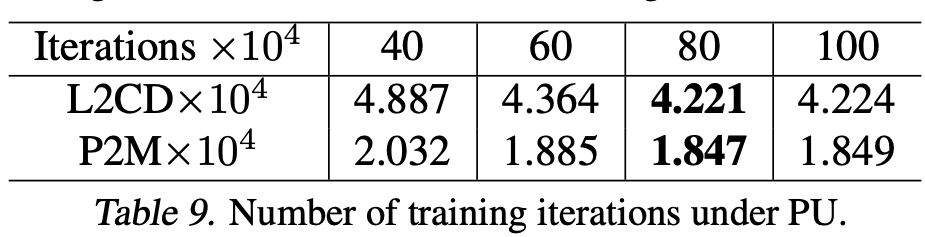
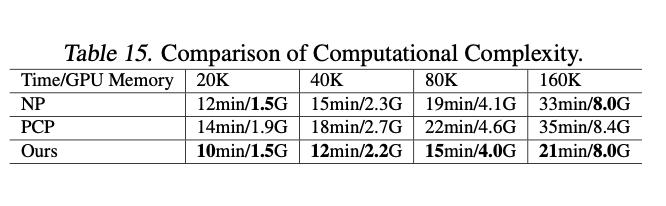
• More corrupted observations are the key to increase the performance of statistical reasoning although one corrupted observation is also fine to perform statistical reasoning well.